Kangaroo

There are two kangaroos on a number line ready to jump in the positive direction. Each kangaroo takes the same amount of time to make a jump, regardless of distance. That is, if kangaroo one jumps 3 meters and kangaroo two jumps 5 meters, they each do it in one second, for example.

Given the starting locations and jump distances for each kangaroo, determine if and when they will land at the same location at the same time.

Input Format

Parametes as integers denoting the respective values of x1, v1, x2, and v2.

Constraints

• $0 \le x1 \le x2 \le 10000$
• $1 \le v1 \le 10000$
• $1 \le v2 \le 10000$

Output Format

Boolean value denoting if they can land on the same location at the same time.

Sample Input

x1 = 0
v1 = 3
x2 = 4
v2 = 2

Sample Output

true

Explanation

The two kangaroos jump through the following sequence of locations:

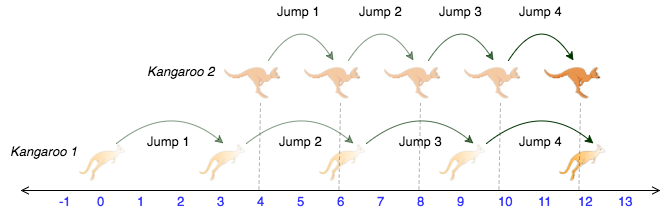
The kangaroos meet after 4 jumps.

Solution

This is a linear equation problem and we can represent them as:

$ k1 = 3x + 0$

$ k2 = 2x + 4$

Therefore:

$3x = 2x + 4$

$x = 4$

The kangaroos meet after 4 jumps. So the equation result must be a positive and whole number in order to fit the requirements.

Code

public class KangarooMeasurer {

	private Boolean measure(
		Integer x1,
		Integer v1,
		Integer x2,
		Integer v2){

		double left = v1 - v2;
		double right = x2 - x1;

		if(left < 0){
			left = left * -1;
			right = right * -1;
		}

		double result = right / left;
		return right > 0 && result % 1 == 0;
	}

	public static void main(String[] args){
		Integer x1 = 0;
		Integer v1 = 3;
		Integer x2 = 4;
		Integer v2 = 2;
		Boolean meets = new KangarooMeasurer().measure(x1, v1, x2, v2);
		assert true == meets;
	}

}

To Download the code:

git clone https://github.com/josdem/algorithms-workshop.git
cd kangaroo

To run the code:

javac KangarooMeasurer.java
java -ea KangarooMeasurer

Return to the main article